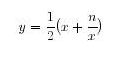"Método de Herón"
Matemáticas 2
Fátima Naveda Priego
Tercer Semestre de Bachillerato Grupo A
Jueves 31 de Agosto del 2017
Prof. Marco Antonio Morales Contreras
Villahermosa, Tabasco
Matemáticas 2
Fátima Naveda Priego
Tercer Semestre de Bachillerato Grupo A
Jueves 31 de Agosto del 2017
Prof. Marco Antonio Morales Contreras
Villahermosa, Tabasco
INTRODUCCIÓN
La presente investigación nos informará acerca de como calcular el área de un triangulo en un plano cartesiano ya que con el método de Herón se vuelve mas útil y accesible.
Asimismo, se pretende abordar el proceso anterior para poder llegar a lo requerido.
A lo largo de su vida, este ingeniero y matemático helenístico, que trabajó en el Musaeum, el museo anexo a la Biblioteca de Alejandría, llegó a idear tales inventos una coleecion de 80 aparatos mecánicos que funcionan con aire, vapor o presión hidráulica‒ que es difícil creer que viviera en el siglo I d. C.
Uno de sus inventos más famosos fue la primera máquina de vapor, conocida como eolípila. Basado en una idea de Vitruvius, La eolípila consistía en una esfera hueca llena de agua a la que se adaptaban dos tubos curvos. El mecanismo tenía debajo un caldero con llamas, de forma que cuando el agua de la esfera llegaba a hervir los tubos expulsaban el vapor, haciendo girar el conjunto a gran velocidad. Herón demostró que su modelo podía tener aplicaciones prácticas y diseñó una versión que servía de puertas automáticas para templos.
Entre los muchos "Herón" que existen en la historia de las ciencias técnico-matemáticas unos de los más importantes fue el de Alejandría (que por cierto parece ser que tampoco nació allí sino en Ascra). Si tiene más fundamento el que era de origen humilde y fue, en su juventud, zapatero. Tampoco existen datos dignos de crédito respecto a su nacimiento (?126 a.C.) ni a su muerte (?50 a.C.).
Aunque quizás la expresión matemática más conocida de Herón sea su fórmula para determinar el área de un triágulo conocidos sus lados. Algo realmente útil en aquellos tiempos. Si bien parece que era conocida por Arquímedes, la primera demostración que nos ha llegado figura en la Métrica uno de los tratados más famosos de Herón. El teorema nos garantiza, conociendo las lados de un triángulo, conocer su área, mediante la expresión de más abajo donde a, b y c son los lados del triángulo y p la mitad del perímetro del mismo.
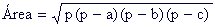
También existe un famoso método de Herón para calcular o aproximar raíces cuadradas. Este método increiblemente moderno, se basa en calcular aproximaciones sucesivas de la raiz cuadrada de un número positivo n. Esto es si x es una aproximación se define la siguiente como
Como es fácil de probar que si |x^2-n|<ε entonces |y^2-n|<ε^2/4. La aproximación, de los sucesivos cuadrados a n, decimos que es cuadrática y en la práctica los sucesivos valores de las aproximaciones convergen muy rápidamente al valor real de √ n.
Para poder encontrar el área, primero tenemos que tener las medidas de los lados; en caso de no tenerlo, aquí te ayudaremos a poder sacar las medidas de un punto a otro para obtener un lado y así sucesivamente poder obtener todos los lados.
La formula para sacar distancia entre un punto y otro es:
Aquí les dejo un video para que sea mas entendida esta parte:
Ya que tienes la medida de un lado, debes continuar calculando los puntos que siguen.
Si es un triangulo equilátero, con calcular solo un lado es mas que suficiente, ya que solo lo sumas 2 veces mas el resultado y listo.
Ya obtenida toda las distancias, se sacará el perímetro
La formula para sacar perímetro es:

Se suman todas las distancias y ya sumado, después se divide entre 2; y ese resultado es el perímetro, que a continuación se va a utilizar.
Aquí dejo un video para que esta explicación quede mas clara.
Y continuando, les mostraré la formula de Herón aplicando el área:

Les dejo un video para que se les facilite la comprensión del ultimo punto tocado:
Aquí les dejo un ejemplo donde utilicé las formulas que les coloqué en la parte superior(donde está la información), pueden agarrar el ejemplo de mi figura como práctica y al final corroborar su resultado; la aplicación que utilicé se llama Geogebra.
CONCLUSIÓN
Podemos observar y analizar que no es complicado el uso de éste método, ya que las formulas están establecidas, y que con el método de Herón podemos hallar de manera fácil las medidas de una figura, y aunque nos encontremos en un plano cartesiano y nos señalen la figura, nosotros mismos podamos resolver el problema, poniendo las distancias, sacando el perímetro, etc.
Hay muchos métodos que podemos utilizar, pero yo recomiendo que utilicen el de Herón, ademas de que encontrarán muchísima información y videos en Internet donde les expliquen el procedimiento.
Espero les haya gustado y dejen un comentario abajo.
Hay muchos métodos que podemos utilizar, pero yo recomiendo que utilicen el de Herón, ademas de que encontrarán muchísima información y videos en Internet donde les expliquen el procedimiento.
Espero les haya gustado y dejen un comentario abajo.
REFERENCIAS BIBLIOGRÁFICAS
Math2me.com. (2017). Perímetro y área de un triángulo│fórmula de Herón @ math2me.com. [online] Available at: http://math2me.com/playlist/geometria/perimetro-y-area-de-un-triangulo-formula-de-heron [Accessed 28 Aug. 2017].
Formulas, U., Formulas, U., Formulas, U. and Formulas, U. (2017). Fórmula de Herón. [online] Universo Formulas. Available at: http://www.universoformulas.com/matematicas/geometria/formula-heron/ [Accessed 28 Aug. 2017].
Profesorenlinea.com.mx. (2017). Distancia entre dos puntos. [online] Available at: http://www.profesorenlinea.com.mx/geometria/Distancia_entre_dos_puntos.html [Accessed 28 Aug. 2017].
Profesorenlinea.com.mx. (2017). Distancia entre dos puntos. [online] Available at: http://www.profesorenlinea.com.mx/geometria/Distancia_entre_dos_puntos.html [Accessed 28 Aug. 2017].